Spacetime Distances
TLDR: Special relativity shows us how to think about spacetime and distances measured with imaginary numbers. Utopia uses units of length that are more obviously connected to light.
Prerequisites: Counting, Timekeeping, basic understanding of geometry, trigonometry, and complex/imaginary numbers
As discussed in the essay on timekeeping, to make clock-making easier, units in Utopia are based around the physical properties of cesium. Specifically, a cold cesium-133 atom will emit light with a specific energy/wavelength when it changes energy levels. This wavelength could alternately be seen as a frequency, and we can measure durations as multiples of that frequency.
This, as it happens, is not just about Utopia — it’s also how Earth units are defined! The length of a second is defined to be exactly 9,192,631,770 times the duration it takes one of these photons to fully oscillate. Utopia just uses a better multiple of the unit, which is less anchored in silly, historical details.
Earth also happens to have a unit of distance — the meter — which we derive from the taking the amount of distance travelled by a photon in one second and then multiplying it by another gross, arbitrary, historical constant: 299,792,458. Even imperial units like inches and miles are secretly anchored on this number; an inch is defined as exactly 2.54 cm.
But this is dumb. Not just because of the gross, historical constants, but because we started with measuring a wavelength of light, converted it into a frequency/duration, then multiplied by the velocity of light to get a distance. But we could have just stuck with the waveLENGTH as the fundamental quantity and gotten a very nice unit as a result. The distance traveled in one full oscillation of cesium-standard light is exactly 3.26122557 centimeters, or approximately 1.28 inches.
In Utopia this is the fundamental unit of length: the standard galactic fingertip. (It sounds cooler in the Utopian universal language.)
1/36 fingertip = 1 wire ≈ 0.91 mm
1/36 wire = 1 fiber ≈ 25 μm
1/36 fiber = 1 red ≈ 699 nm
1/36 red = 1 biomachine ≈ 19.4 nm
1/36 biomachine = 1 molecule ≈ 0.54 nm
36 fingertips = 1 stretch ≈ 117.4 cm ≈ 46 inches
36 stretches = 1 tower ≈ 42.3 m ≈ 140 feet
36 towers = 1 (Standard Galactic) mile ≈ 1.52 km ≈ 0.95 miles
36 (SG) miles = 1 ride ≈ 55 km ≈ 34 miles
36 rides = 1 border ≈ 1972 km ≈ 1225 miles
Even though Utopia doesn’t divide the world into countries like we do, it’s still convenient to talk about different regions and territories. A “region” is then a unit of square-area — specifically a square “border” ≈ 3,889,000 km² ≈ 1,500,000 mi² ≈ 1 billion acres ≈ the area of Europe ≈ 1/2 the area of the continental USA.
Note that just like in English, we can convert back-and-forth between durations and distances (e.g. “light-year”). 36 standard galactic borders is equal to a light-blink, just like a light-mile is equal to 1/6⁶ of a standard galactic blink. In fact, units of time are set up to use light-distances for small units of time, just like large units of space are set up to use light-times.
There are many reasons we could explore for why we use the speed of light to connect space and time, rather than some other (less-extreme) velocity. But I think the best story comes from relativistic physics, which tells us that in a very important sense time and space are measured with the same type of units.
Space
To understand this, let’s first consider a view of the universe that’s frozen in time and contemplate how we think about space. One common perspective is to think about objects in space as superimposed on a 3-dimensional grid with a distinct origin point, almost like graph paper or Minecraft. A location can then be described by referencing the position of a point by giving the number of units in each direction to move from the origin to get to that spot. This mathematical object is called a Euclidean space.
But the universe isn’t a Euclidean space. Not really. The most obvious reasons why are that there are no objectively-correct choices for where to put the origin point or which units to use to make the grid. One person might measure from Rome using miles while another would measure from Mecca using feet. Even the orientation of the grid is arbitrary — rotating the grid doesn’t change the contents, only how we describe them.
Reality does, however, pin down the relative distances between points. Relative distances are unitless — measuring in miles or feet won’t change which destinations are twice as far away from a starting point. This mathematical object — a Euclidean space where we’ve “forgotten” where the origin is or what the units are, and we can only check relative distances, is called an affine space1.
In practice we usually describe reality by inventing a Euclidean basis where we can show how the relative distances from the affine space are being faithfully represented. The numbers of a coordinate system are just too useful to give up! But the key is that approximately all the Euclidean details are artificial — only the relative distances are real (i.e. observer-independent).
(Warning: Just because reality is better described by an affine space, doesn’t mean it’s best described that way. We’ll get into the ways in which the math fails us towards the end of the essay.)
Let’s recall that standard distance in 3D Euclidean space is defined to be:dist((x₁,y₁,z₁), (x₂,y₂,z₂)) ≔ √((x₂-x₁)² + (y₂-y₁)² + (z₂-z₁)²)
But now let’s imagine that we’ve invented a basis for reality where we use different units for the different dimensions. Like, let’s say we measure the x-coordinate in meters, the y-coordinate in leagues, and the z-coordinate in fleepdorps. This ruins the distance calculation! In order to make things work, I need to convert all the dimensions into the same unit. The only sane thing to do is to just use the same type of unit in the first place.
Weirdo Spaces
Before moving along, I want to see if we can generalize the notion of affine space a bit. Again, an affine space is like a Euclidean space where we give points numerical coordinates, but we treat the specific numbers as artifacts and only concern ourselves with the relative distances.
Notice, however, that preserving relative distance is equivalent to preserving relative squared-distance2. Let's say I have two reference points, like the center of London and the center of Prague. If I know the squared-distance between, say Tokyo and London as a multiple of squared London-Prague distances, then I also know the distance from Tokyo to London as a multiple of the distance from London to Prague. It's just the (positive) square-root of the relative square-distance.
dist(L,P) ≈ 1,000 km
dist(L,P)² ≈ 1,000,000 km²
dist(T,L)²/dist(L,P)² ≈ 100
dist(T,L)/dist(L,P) ≈ √100 = 10In general, if knowing your distance (or relative squared-distance) to a pair of (well-chosen3) reference points is enough to pin down your location, you're in a one-dimensional world. If you need three reference points, it means you’re in a two-dimensional world. And again for four reference points and 3D space.

Now let’s drop the assumption that squared distances must be non-negative. What happens? Well, we must have imaginary numbers as distances some of the time. But what does that change? If we treated “imaginary distances” similarly to “real distances” does anything break?
Imagine if we, in London, could somehow measure the squared distance to Xanadu in terms of the squared distance to Prague. And let’s suppose that our measuring device says the relative square-distance is -1. In other words:
dist(L,X)²/dist(L,P)² ≈ -1
dist(L,X)/dist(L,P) ≈ i
dist(L,X) ≈ dist(L,P) × i ≈ 1,000 km × iThis is weird, but not incoherent. We’ve certainly added another dimension to our universe, but the math keeps on chugging along. The biggest problem is visualization. It’s easy to have geometric intuitions about distances, but “imaginary distances” don’t make obvious sense.
Or do they…
Time
Time is weird.
If I want to meet you around a point, we need to be nearby in the dimensions of space, but also in time. So it’s tempting to just say that we have a 4-dimensional affine space where time is one of the dimensions. But that can’t be right… The laws of physics treat all the dimensions of space identically — this is why there’s no right answer to which-way-the-grid-goes. But time is definitely distinct from space! For starters, there’s conservation of momentum and energy across time, but definitely not across space. Rotations that exchange one direction for another make sense, but what would a rotation-in-time look like?
In the olden-days people like Galileo used to model the points in the world as belonging to both a 3D affine space for position, and a 1D space for time. But Einstein showed that this is basically just wrong. There are many consequences of special relativity, but the theoretical take-away for our purposes is that reality is instead better (but not best!) modeled by a 4D affine space where distances along exactly one dimension4 are imaginary, just like we explored in the previous section. In other words, the right way to visualize an “imaginary distance” is as indicating that the thing you’re measuring to is (mostly) in the past/future.
How do we know that this is the right way to think about the world? Well, the physical evidence behind Einstein’s (special) relativity is beyond the scope of this essay, but let’s consider how if we use this math to think about spacetime we get a bunch of cool theoretical properties.
The artifacts that arise from modeling an affine space in some Euclidean basis can be alternately conceived as observer-specific features. For instance, the free choice of origin corresponds to the universe being the same regardless of where and when you’re observing it from. The free choice of scale and rotation corresponds to the universe being able to equally be observed from any angle and using any choice of units.
Now, regardless of whether you conceptualize spacetime like Einstein or Galileo, we can imagine each object as following a path through spacetime. If that path is a straight line, we can say that the object has a fixed velocity — we can predict where it will be at a future time by considering how it’s moving beforehand. A straight path that’s parallel to the time-axis corresponds to a stationary object. Thus velocity is not a question of magnitude — only one of direction in spacetime.
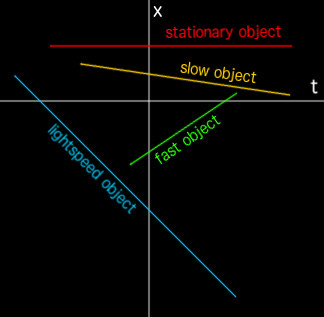
In Galileo’s conception of time all paths/velocities should be equally skewed when an observer accelerates. But this isn’t what we actually see! The observed velocity of light doesn’t depend on observer. No matter how fast you try to go, the speed of light will stay constant.
This property falls out of the math automatically when we have an imaginary dimension in an otherwise simple affine space. The key feature of translations, rotations, zooms, and reflections is that they all preserve relative distances. A rotation in time is exactly the same — the velocities of objects going slower than lightspeed change relative to the observer, but they change such that the distance between points along those object’s paths in spacetime remains fixed.
Tick-Tock
Consider an example of a clock that’s sitting still relative to some observer we’ll call Alice. Since the clock is at rest from her perspective, Alice models the clock’s path through spacetime as parallel with the time axis.
Another observer we’ll call Bob sees the same universe, but Bob is moving at 58%5 the speed of light compared to Alice and the clock. From his perspective he is stationary and the clock is shooting rapidly through space with a spacetime path at a 30-degree angle from the time-axis (100% the speed of light = 45 degrees). Neither Alice nor Bob are “right” about what speed the clock is moving, only about what speed it is moving relative to them. There is no such thing as absolute speed.
Bob must see the same spacetime distances between clock-ticks as Alice. Let’s consider a point in the clock’s path that Alice sees as “a” units of the grid after when the clock shows 1:00. The distance must then be a×i (since distances in time are imaginary). But the distance is also some quantity “b” along the 30° trajectory:
Alice's Notion of Distance = Bob's Notion of Distance
√((a×sin(0°))² + (a×i×cos(0°))²) = √((b×sin(30°))² + (b×i×cos(30°))²)
(a×sin(0°))² + (a×i×cos(0°))² = (b×sin(30°))² + (b×i×cos(30°))²
0 - a² = b²/4 - 3b²/4
-a² = -2b²/4
a² = b²/2
b² = 2a²
b = √2 × aFrom Bob’s perspective the clock ticks more slowly! Time dilation (and length contraction) emerges as a natural consequence of preserving spacetime distances!
In general, when an object appears moving to some observer, the object’s internal motion (e.g. clock ticks, aging, thoughts, etc.) will appear to be slowed down by a factor of √(1 - v²), where v is the object’s speed expressed in the natural units. Thus a clock traveling at 60% the speed of light will appear to tick at √(1 - 0.6²) = √(1 - 0.36) = √0.64 = 0.8 = 80% of the speed that it would if it was at rest (relative to the observer).
We can also use this math to see why the speed of light is constant, regardless of the speed of the observer’s coordinate system. All points on the path of a photon have a distance of 0 from each other! (Proof in footnote6.) If we could make the speed of a photon decrease then those points would have non-zero distance, which would violate our invariants. Thus no transformation can make a non light-like path into a light-like path or vice-versa. Similarly, all slower-than-light paths have negative squared-distance, and faster-than-light paths have positive squared-distance, so there's no transformation that can take an object's path faster than the speed of light.
Note that this way of calculating only works if time and space use comparable units. Meaning a distance of one light-second must be naturally the same length as a duration of one second. Time and space aren’t the same, of course! There’s a factor of √-1 connecting the two, but √-1 is unitless — the units of time and space are ultimately the same (if we’re being sensible).
Symmetries and Affine Caveats
At the risk of overloading you, I feel that there are a couple warning caveats around affine spaces that I should hit before wrapping up, especially if I’m hoping to pass the Onion Test.
The first is that affine spaces are flat, being basically Euclidean spaces where the grid has been erased. For instance, in a standard notion of affine space, parallel lines will never meet. But the universe probably isn’t flat — it’s merely locally flat. Consider the surface of the Earth, which appears flat (ignoring tides and land and such), but parallel lines of longitude all meet at the poles. In a similar way, gravity is the reshaping of the curvature of spacetime, such that parallel lines of motion in our universe (e.g. two objects falling straight down) can end up converging.
This doesn’t change the idea that that the relative distances between things is what’s real. It just means that we can’t make additional assumptions given those relative distances.
The second and final warning I want to give relates to symmetries. As I mentioned earlier, many symmetries of the universe could be described as being a product of the artifacts that a Euclidean perspective brings. For instance, translational symmetry means that if we move everything in the universe “to the left,” nothing changes, and this falls out immediately from an awareness of how “to the left” can only make sense when relating a bunch of objects within the universe, since there’s not actually a grid/origin from which to compare.
But if you take this story seriously, you can mess up and assume a symmetry that isn’t actually there. One of the most important experiments ever done in physics was the breaking of parity-symmetry by Chien-Shiung Wu in 1956. (Side note: Wu is another great example of a scientist whose work is underrated because she was more of a laboratorist than a theorist.) For a long time it was assumed that one could negate all the coordinates along a certain dimension (or all spacial dimensions) and get an equally-good picture of reality — all the distances are preserved under reflection after all. And nearly every force and interaction seems respect flipping in this way… except for the weak nuclear interaction.
Thus, while a Euclidean spacetime is certainly wrong, even a curved affine spacetime is very likely leaving things out. That said, I’m less convinced that parity-symmetry is actually broken than most people, and I may eventually write an essay going into my wildly contrarian perspective there.
Utopian Distances
In the Utopia it’s common knowledge that lengths of time and lengths of distance are both lengths, united by a factor of √-1 (or 1/i (aka -√-1) when going the other way). In fact, the Utopian language calls imaginary numbers “temporal numbers” and introduces them to students in the context of spacetime, so that they feel more justified as a useful concept.
Though most human-scale distances are measured in units named after familiar objects like fingertips and towers, it’s common to measure very long distances in the time it takes light to travel that far.
The “speed of light” is not named as such, or conceived as such in Utopia. Instead, it’s simply called “fullspeed,” since it’s the speed at which all fields propagate. Utopian physicists use these better units, and thus have many simpler formulae and have an easier time explaining to students the nature of entities like momentum and energy.
Affine spaces are pretty easy to define, but my favorite affine space approximation, using a notation based on dependent type theory, is: (Point : Set) & (r : (o : Point) → (p : Point, p ≠ o) → (q : Point, q ≠ o) → ℝ⁺) & (∀ o p q. r o p q = 1/(r o q p)) & (∀ o p q, p ≠ q. r q o p = (r p o q)/(r o p q)). Or more plainly, this pseudo-affine space is a set of points and a function that takes three points (o, p, and q) (such that o is not p or q) and returns a positive real number with some laws that restrict what functions are allowed. This function, conceptually, returns how much longer the distance from o to q is than the distance from o to p, or equivalently it gives the distance from o to p in units of o to q distances (i.e. r o p q = dist(o,p)/dist(o,q)).
There is a trivial pseudo-affine space with no points, and another obvious space with only one point. At two points we’re still pretty simple — the r function must always return 1, since it’s the only positive real number that’s its own reciprocal. Only once we have three points do things get at all interesting. Consider this definition for r:r a b c ≔ 2
r b a c ≔ 3
This definition is complete. By our final law we know: r c a b = r b a c / r a b c = 2/3. All other values (1/2, 1/3, 3/2, and a bunch of 1s) follow from reciprocality.
This space isn’t an affine space — it has no notion of vectors, and doesn’t even need to be continuous. That’s what I like about it! It strips things down to the bare-bones, preserving relative distances while allowing reality to be discrete, finite, et cetera.
Using the construction from the previous footnote, we can see that since the squaring-function is strictly monotonic (on non-negative numbers) there’s an isomorphism between pseudo-affine spaces built on r and ones built on r².
Reference points need to not be a weighted average of previous reference points. This is the affine version of linear-independence of basis vectors.
It’s actually equivalent to formalize space as having three imaginary dimensions for space and one non-imaginary dimension for time, and some people do it this way! I think it’s a bit backwards, and prefer time to be the only imaginary dimension.
In an earlier draft of this post I made the mistake of assuming that since 100% of lightspeed makes a 45° angle with the t-axis, a velocity that makes a 30° angle must be 2/3 the speed of light. This is embarrassingly wrong. The angle is that of a right triangle with an adjacent length of 1 and an opposite length of the velocity, a.k.a. the arctangent of the velocity. 58% is approximately arctan(30°); more precisely it’s 1/√3.
Consider two points a and b on a photon’s path. We are allowed to choose an arbitrary origin for our coordinate system, so we choose the origin such that it’s at a. We are allowed to choose any spacial rotation/reflection, so we choose the one where the photon is traveling along the x-axis in the positive direction. The x-coordinate of b will be t units out from the origin (i.e. along the diagonal), where t is the real-coefficient of the time coordinate. Thus: dist((t,0,0,t√-1),(0,0,0,0)) = √(t² - t²) = 0


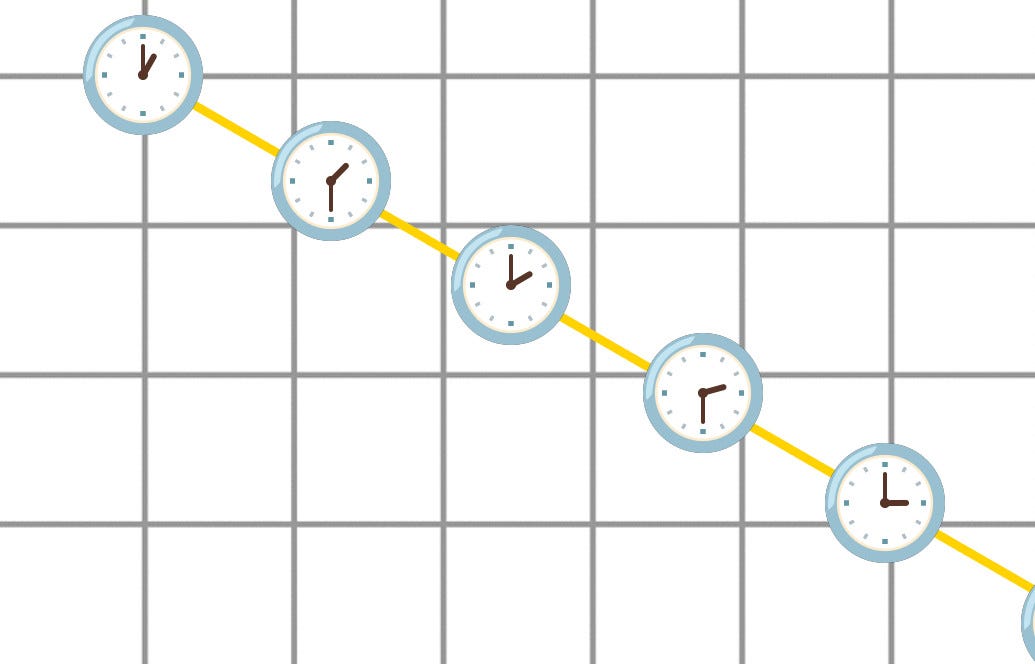
Nitpick: How do you deal with relativistic length contraction? Does length usually refer to proper length (that is length of an object is the object's length in the object's rest frame)?